跳转至

快速开始

AI Studio快速体验

本文通过一个简单的 demo 及其扩展问题，介绍如何使用 PaddleScience 训练模型，解决一类方程学习与预测问题，并可视化预测结果。

1. 问题简介

假设我们希望用神经网络模型去拟合 \(x \in [-\pi, \pi]\) 区间内，\(u=\sin(x)\) 这一函数。在拟合函数已知和未知两种情形下，如何去尽可能地准确拟合 \(u=\sin(x)\)。

第一种场景下，假设已知目标函数 \(u\) 的解析解就是 \(u=\sin(x)\)，我们采用监督训练的思路，直接用该公式生成标签因变量 \(u\)，与自变量 \(x\) 共同作为监督数据对模型进行训练。

第二种场景下，假设不知道目标函数 \(u\) 的解析解，但我们知道其满足某种微分关系，我们这里以其中一个满足条件的微分方程 \(\dfrac{\partial u} {\partial x}=\cos(x)\) 为例，介绍如何生成数据进行训练。

2. 场景一

目标拟合函数：

\[ u=\sin(x), x \in [-\pi, \pi]. \]

我们生成 \(N\) 组数据对 \((x_i, u_i), i=1,...,N\) 作为监督数据进行训练即可。

在撰写代码之前，我们首先导入必要的包。

1
2
import ppsci
from ppsci.utils import logger

然后创建日志和模型保存目录供训练过程记录和保存使用，这一步是绝大部分案例在正式开始前都需要进行的操作。

 6
 7
 8
 9
10
11
12
13
# set random seed(42) for reproducibility
ppsci.utils.misc.set_random_seed(42)

# set output directory
OUTPUT_DIR = "./output_quick_start_case1"

# initialize logger while create output directory
logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info")

接下来正式开始撰写代码。

首先定义问题区间，我们使用 ppsci.geometry.Interval 定义一个线段几何形状，方便后续在该线段上对 \(x\) 进行采样。

15
16
17
# set 1D-geometry domain([-π, π])
l_limit, r_limit = -np.pi, np.pi
x_domain = ppsci.geometry.Interval(l_limit, r_limit)

然后定义一个简单的 3 层 MLP 模型。

19
20
# set model to 3-layer MLP
model = ppsci.arch.MLP(("x",), ("u",), 3, 64)

上述代码表示模型接受自变量 \(x\) 作为输入，输出预测结果 \(\hat{u}\)

然后我们定义已知的 \(u=\sin(x)\) 计算函数，作为 ppsci.constraint.InteriorConstraint 的参数，用于计算标签数据，InteriorConstraint 表示以给定的几何形状或数据集中的数据作为输入，联合给定的标签数据，指导模型进行优化。

22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# standard solution of sin(x)
def sin_compute_func(data: dict):
    return np.sin(data["x"])


# set constraint on 1D-geometry([-π, π])
ITERS_PER_EPOCH = 100  # use 100 iterations per training epoch
interior_constraint = ppsci.constraint.InteriorConstraint(
    output_expr={"u": lambda out: out["u"]},
    label_dict={"u": sin_compute_func},
    geom=x_domain,
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 32,  # use 32 samples(points) per iteration for interior constraint
    },
    loss=ppsci.loss.MSELoss(),
)
# wrap constraint(s) into one dict
constraint = {
    interior_constraint.name: interior_constraint,
}

此处的 interior_constraint 表示一个训练目标，即我们希望在 \([-\pi, \pi]\) 这段区间内，优化模型让模型的预测结果 \(\hat{u}\) 尽可能地接近它的标签值 \(u\)。

接下来就可以开始定义模型训练相关的内容，比如训练轮数、优化器、可视化器。

48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
# set training hyper-parameters
EPOCHS = 10
# set optimizer
optimizer = ppsci.optimizer.Adam(2e-3)(model)

# set visualizer
visual_input_dict = {
    "x": np.linspace(l_limit, r_limit, 1000, dtype="float32").reshape(1000, 1)
}
visual_input_dict["u_ref"] = np.sin(visual_input_dict["x"])
visualizer = {
    "visualize_u": ppsci.visualize.VisualizerScatter1D(
        visual_input_dict,
        ("x",),
        {"u_pred": lambda out: out["u"], "u_ref": lambda out: out["u_ref"]},
        prefix="u=sin(x)",
    ),
}

最后将上述定义的对象传递给训练调度类 Solver，即可开始模型训练

67
68
69
70
71
72
73
74
75
76
77
78
# initialize solver
solver = ppsci.solver.Solver(
    model,
    constraint,
    OUTPUT_DIR,
    optimizer,
    epochs=EPOCHS,
    iters_per_epoch=ITERS_PER_EPOCH,
    visualizer=visualizer,
)
# train model
solver.train()

训练完毕后再用刚才取的 1000 个点与标准解计算 L2-相对误差

81
82
83
84
85
86
# compute l2-relative error of trained model
pred_u = solver.predict(visual_input_dict, return_numpy=True)["u"]
l2_rel = np.linalg.norm(pred_u - visual_input_dict["u_ref"]) / np.linalg.norm(
    visual_input_dict["u_ref"]
)
logger.info(f"l2_rel = {l2_rel:.5f}")

再对这 1000 个点的预测结果进行可视化

88
89
# visualize prediction after finished training
solver.visualize()

训练记录下所示

...
...
ppsci INFO: [Train][Epoch  9/10][Iter  80/100] lr: 0.00200, loss: 0.00663, EQ: 0.00663, batch_cost: 0.00180s, reader_cost: 0.00011s, ips: 17756.64, eta: 0:00:00
ppsci INFO: [Train][Epoch  9/10][Iter  90/100] lr: 0.00200, loss: 0.00598, EQ: 0.00598, batch_cost: 0.00180s, reader_cost: 0.00011s, ips: 17793.97, eta: 0:00:00
ppsci INFO: [Train][Epoch  9/10][Iter 100/100] lr: 0.00200, loss: 0.00547, EQ: 0.00547, batch_cost: 0.00179s, reader_cost: 0.00011s, ips: 17864.08, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  10/100] lr: 0.00200, loss: 0.00079, EQ: 0.00079, batch_cost: 0.00182s, reader_cost: 0.00012s, ips: 17547.05, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  20/100] lr: 0.00200, loss: 0.00075, EQ: 0.00075, batch_cost: 0.00183s, reader_cost: 0.00011s, ips: 17482.92, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  30/100] lr: 0.00200, loss: 0.00077, EQ: 0.00077, batch_cost: 0.00182s, reader_cost: 0.00011s, ips: 17539.51, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  40/100] lr: 0.00200, loss: 0.00074, EQ: 0.00074, batch_cost: 0.00182s, reader_cost: 0.00011s, ips: 17587.51, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  50/100] lr: 0.00200, loss: 0.00071, EQ: 0.00071, batch_cost: 0.00182s, reader_cost: 0.00011s, ips: 17563.59, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  60/100] lr: 0.00200, loss: 0.00070, EQ: 0.00070, batch_cost: 0.00182s, reader_cost: 0.00011s, ips: 17604.60, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  70/100] lr: 0.00200, loss: 0.00074, EQ: 0.00074, batch_cost: 0.00181s, reader_cost: 0.00011s, ips: 17699.28, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  80/100] lr: 0.00200, loss: 0.00077, EQ: 0.00077, batch_cost: 0.00180s, reader_cost: 0.00011s, ips: 17764.92, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  90/100] lr: 0.00200, loss: 0.00075, EQ: 0.00075, batch_cost: 0.00180s, reader_cost: 0.00011s, ips: 17795.87, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter 100/100] lr: 0.00200, loss: 0.00071, EQ: 0.00071, batch_cost: 0.00179s, reader_cost: 0.00011s, ips: 17872.00, eta: 0:00:00

训练完毕后再用刚才取的 1000 个点与标准解计算 L2-相对误差

81
82
83
84
85
86
# compute l2-relative error of trained model
pred_u = solver.predict(visual_input_dict, return_numpy=True)["u"]
l2_rel = np.linalg.norm(pred_u - visual_input_dict["u_ref"]) / np.linalg.norm(
    visual_input_dict["u_ref"]
)
logger.info(f"l2_rel = {l2_rel:.5f}")

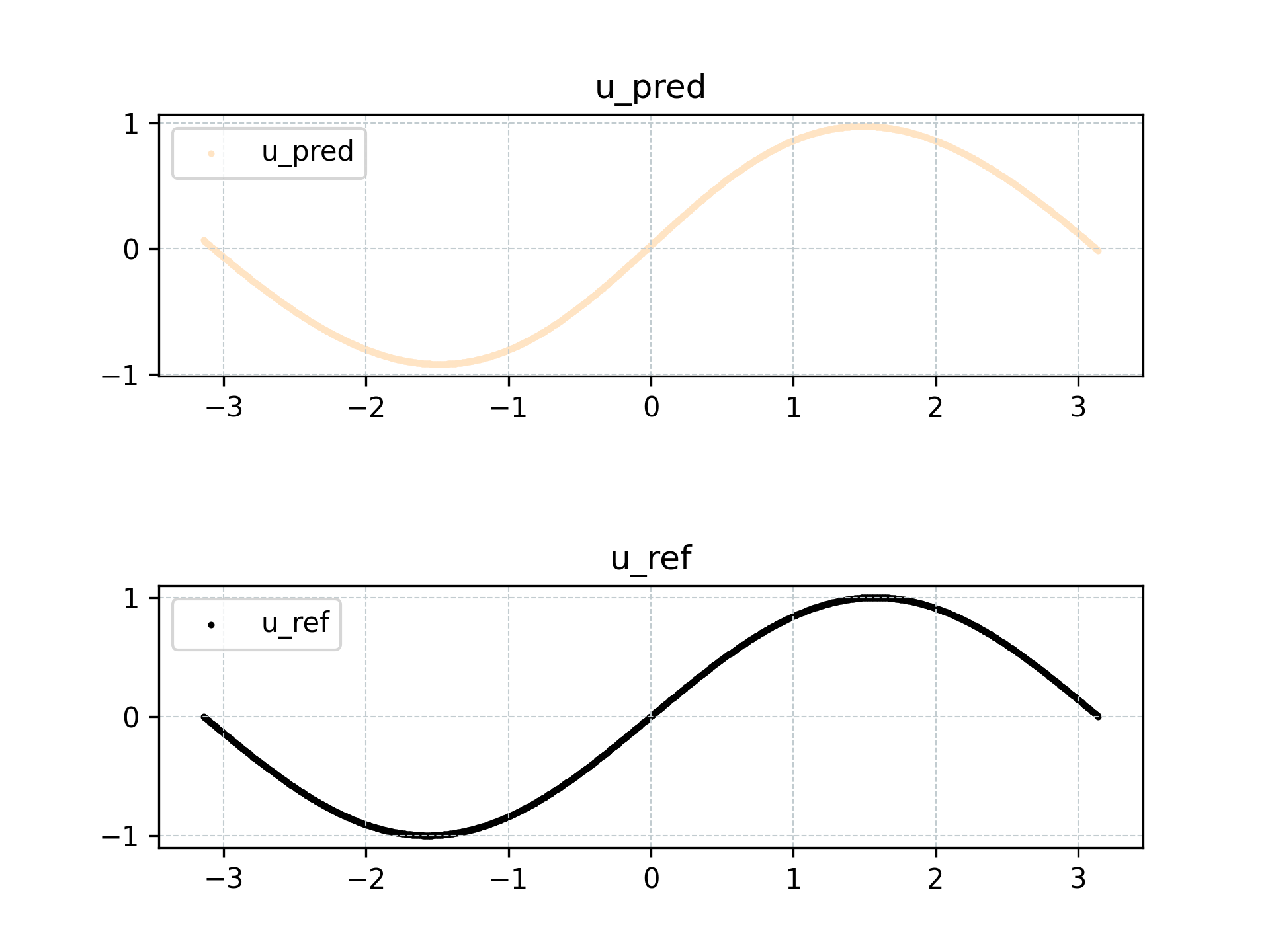
可以看到利用标准解监督训练模型，在标准解附近仍有很好的预测能力，L2-相对误差为 0.02677。

预测结果可视化如下所示

u=sin(x) prediction

场景一的完整代码如下所示

examples/quick_start/case1.py
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
import numpy as np

import ppsci
from ppsci.utils import logger

# set random seed(42) for reproducibility
ppsci.utils.misc.set_random_seed(42)

# set output directory
OUTPUT_DIR = "./output_quick_start_case1"

# initialize logger while create output directory
logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info")

# set 1D-geometry domain([-π, π])
l_limit, r_limit = -np.pi, np.pi
x_domain = ppsci.geometry.Interval(l_limit, r_limit)

# set model to 3-layer MLP
model = ppsci.arch.MLP(("x",), ("u",), 3, 64)

# standard solution of sin(x)
def sin_compute_func(data: dict):
    return np.sin(data["x"])


# set constraint on 1D-geometry([-π, π])
ITERS_PER_EPOCH = 100  # use 100 iterations per training epoch
interior_constraint = ppsci.constraint.InteriorConstraint(
    output_expr={"u": lambda out: out["u"]},
    label_dict={"u": sin_compute_func},
    geom=x_domain,
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 32,  # use 32 samples(points) per iteration for interior constraint
    },
    loss=ppsci.loss.MSELoss(),
)
# wrap constraint(s) into one dict
constraint = {
    interior_constraint.name: interior_constraint,
}

# set training hyper-parameters
EPOCHS = 10
# set optimizer
optimizer = ppsci.optimizer.Adam(2e-3)(model)

# set visualizer
visual_input_dict = {
    "x": np.linspace(l_limit, r_limit, 1000, dtype="float32").reshape(1000, 1)
}
visual_input_dict["u_ref"] = np.sin(visual_input_dict["x"])
visualizer = {
    "visualize_u": ppsci.visualize.VisualizerScatter1D(
        visual_input_dict,
        ("x",),
        {"u_pred": lambda out: out["u"], "u_ref": lambda out: out["u_ref"]},
        prefix="u=sin(x)",
    ),
}

# initialize solver
solver = ppsci.solver.Solver(
    model,
    constraint,
    OUTPUT_DIR,
    optimizer,
    epochs=EPOCHS,
    iters_per_epoch=ITERS_PER_EPOCH,
    visualizer=visualizer,
)
# train model
solver.train()

# compute l2-relative error of trained model
pred_u = solver.predict(visual_input_dict, return_numpy=True)["u"]
l2_rel = np.linalg.norm(pred_u - visual_input_dict["u_ref"]) / np.linalg.norm(
    visual_input_dict["u_ref"]
)
logger.info(f"l2_rel = {l2_rel:.5f}")

# visualize prediction after finished training
solver.visualize()

3. 场景二

可以看到场景一的监督训练方式能较好地解决函数拟合问题，但一般情况下我们是无法得知拟合函数本身的解析式的，因此也无法直接构造因变量的监督数据。

虽然无法求出解析式直接构造监督数据，但往往可以利用相关数学知识，推导出目标拟合函数符合的某种数学关系，以训练模型以满足这种数学关系的方式，达到以“间接监督”的方式优化模型的目的。

假设我们不再使用 \(u=\sin(x)\) 这一先验公式，因而无法计算标签数据 \(u\)。因此使用如下方程组，其含有一个偏微分方程和边界条件

\[ \begin{cases} \begin{aligned} \dfrac{\partial u} {\partial x} &= \cos(x) \\ u(-\pi) &= 2 \end{aligned} \end{cases} \]

构造数据对 \((x_i, \cos(x_i)), i=1,...,N\)。 这意味着我们仍然能保持模型的输入、输出不变，但优化目标变成了：让 \(\dfrac{\partial \hat{u}} {\partial x}\) 尽可能地接近 \(\cos(x)\)，且 \(\hat{u}(-\pi)\) 也要尽可能地接近 \(2\)。

基于以上理论，我们对场景一的代码进行少量的改写即可得到本场景二的代码。

首先由于我们需要使用一阶微分这一操作，因此在代码开头处需导入一阶微分 API

1
2
3
import ppsci
from ppsci.autodiff import jacobian
from ppsci.utils import logger

然后在原来的标签计算函数下方，新增一个微分标签值计算函数

28
29
30
# standard solution of cos(x)
def cos_compute_func(data: dict):
    return np.cos(data["x"])

接着将 interior_constraint 这一约束条件从约束“模型输出”，改为约束“模型输出对输入的一阶微分”

33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# set constraint on 1D-geometry([-π, π])
ITERS_PER_EPOCH = 100  # use 100 iterations per training epoch
interior_constraint = ppsci.constraint.InteriorConstraint(
    output_expr={"du_dx": lambda out: jacobian(out["u"], out["x"])},
    label_dict={"du_dx": cos_compute_func},
    geom=x_domain,
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 32,  # use 32 samples(points) per iteration for interior constraint
    },
    loss=ppsci.loss.MSELoss(),
)

考虑到一般情况下偏微分方程的解会存在待定系数，需通过定解条件（初（边）值条件）来确定，因此需要在 interior_constraint 构建代码的后面，额外添加一个边界条件约束 bc_constraint，如下所示

50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
bc_constraint = ppsci.constraint.BoundaryConstraint(
    {"u": lambda d: d["u"]},
    {"u": lambda d: sin_compute_func(d) + 2},  # (1)
    x_domain,
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 1,  # use 1 sample(point) per iteration for boundary constraint
    },
    loss=ppsci.loss.MSELoss(),
    criteria=lambda x: np.isclose(x, l_limit),
)
  1. 对应边界条件 \(u(x_0)=sin(x_0)+2\)

然后将该边界约束 bc_constraint 添加到 constraint 中

66
67
68
69
70
# wrap constraint(s) into one dict
constraint = {
    interior_constraint.name: interior_constraint,
    bc_constraint.name: bc_constraint,
}

同样地，修改 Visualizer 绘制的标准解为 \(sin(x)+2\)

77
78
79
80
81
82
83
84
85
86
87
88
89
# set visualizer
visual_input_dict = {
    "x": np.linspace(l_limit, r_limit, 1000, dtype="float32").reshape(1000, 1)
}
visual_input_dict["u_ref"] = np.sin(visual_input_dict["x"]) + 2.0
visualizer = {
    "visualize_u": ppsci.visualize.VisualizerScatter1D(
        visual_input_dict,
        ("x",),
        {"u_pred": lambda out: out["u"], "u_ref": lambda out: out["u_ref"]},
        prefix="u=sin(x)",
    ),
}

修改完毕后执行训练

 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
# initialize solver
solver = ppsci.solver.Solver(
    model,
    constraint,
    OUTPUT_DIR,
    optimizer,
    epochs=EPOCHS,
    iters_per_epoch=ITERS_PER_EPOCH,
    visualizer=visualizer,
)
# train model
solver.train()

训练日志如下所示

...
...
ppsci INFO: [Train][Epoch  9/10][Iter  90/100] lr: 0.00200, loss: 0.00176, EQ: 0.00087, BC: 0.00088, batch_cost: 0.00346s, reader_cost: 0.00024s, ips: 9527.80, eta: 0:00:00
ppsci INFO: [Train][Epoch  9/10][Iter 100/100] lr: 0.00200, loss: 0.00170, EQ: 0.00087, BC: 0.00083, batch_cost: 0.00349s, reader_cost: 0.00024s, ips: 9452.07, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  10/100] lr: 0.00200, loss: 0.00107, EQ: 0.00072, BC: 0.00035, batch_cost: 0.00350s, reader_cost: 0.00025s, ips: 9424.75, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  20/100] lr: 0.00200, loss: 0.00116, EQ: 0.00083, BC: 0.00033, batch_cost: 0.00350s, reader_cost: 0.00025s, ips: 9441.33, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  30/100] lr: 0.00200, loss: 0.00103, EQ: 0.00079, BC: 0.00024, batch_cost: 0.00355s, reader_cost: 0.00025s, ips: 9291.90, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  40/100] lr: 0.00200, loss: 0.00108, EQ: 0.00078, BC: 0.00030, batch_cost: 0.00353s, reader_cost: 0.00025s, ips: 9348.09, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  50/100] lr: 0.00200, loss: 0.00163, EQ: 0.00082, BC: 0.00082, batch_cost: 0.00350s, reader_cost: 0.00024s, ips: 9416.24, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  60/100] lr: 0.00200, loss: 0.00160, EQ: 0.00083, BC: 0.00077, batch_cost: 0.00353s, reader_cost: 0.00024s, ips: 9345.73, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  70/100] lr: 0.00200, loss: 0.00150, EQ: 0.00082, BC: 0.00068, batch_cost: 0.00351s, reader_cost: 0.00024s, ips: 9393.89, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  80/100] lr: 0.00200, loss: 0.00146, EQ: 0.00081, BC: 0.00064, batch_cost: 0.00350s, reader_cost: 0.00024s, ips: 9424.81, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter  90/100] lr: 0.00200, loss: 0.00138, EQ: 0.00081, BC: 0.00058, batch_cost: 0.00349s, reader_cost: 0.00024s, ips: 9444.12, eta: 0:00:00
ppsci INFO: [Train][Epoch 10/10][Iter 100/100] lr: 0.00200, loss: 0.00133, EQ: 0.00079, BC: 0.00054, batch_cost: 0.00349s, reader_cost: 0.00024s, ips: 9461.54, eta: 0:00:00

训练完毕后再用刚才取的 1000 个点与标准解计算 L2-相对误差

104
105
106
107
108
109
# compute l2-relative error of trained model
pred_u = solver.predict(visual_input_dict, return_numpy=True)["u"]
l2_rel = np.linalg.norm(pred_u - visual_input_dict["u_ref"]) / np.linalg.norm(
    visual_input_dict["u_ref"]
)
logger.info(f"l2_rel = {l2_rel:.5f}")

可以看到利用微分方程训练的模型，在标准解附近仍有很好的预测能力，L2-相对误差为 0.00564。

预测结果可视化如下所示

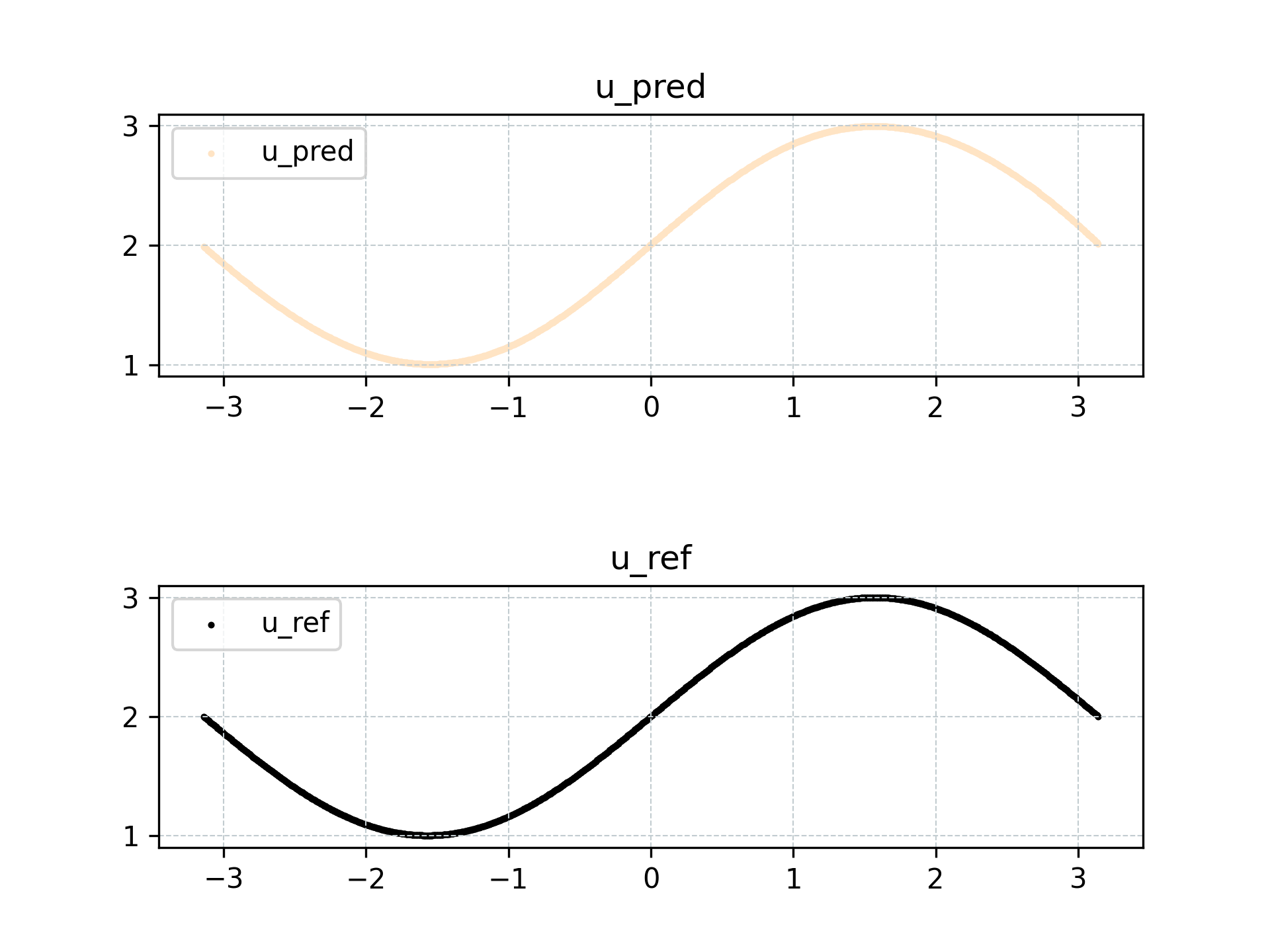
u=sin(x)+2 prediction

可以发现利用微分关系训练的模型仍然具备良好的预测能力，并且结合定解条件，能学习出同时符合微分方程和定解条件的正确解模型。

场景二的完整代码如下所示

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
import numpy as np

import ppsci
from ppsci.autodiff import jacobian
from ppsci.utils import logger

# set random seed(42) for reproducibility
ppsci.utils.misc.set_random_seed(42)

# set output directory
OUTPUT_DIR = "./output_quick_start_case2"

# initialize logger while create output directory
logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info")

# set 1D-geometry domain([-π, π])
l_limit, r_limit = -np.pi, np.pi
x_domain = ppsci.geometry.Interval(l_limit, r_limit)

# set model to 3-layer MLP
model = ppsci.arch.MLP(("x",), ("u",), 3, 64)

# standard solution of sin(x)
def sin_compute_func(data: dict):
    return np.sin(data["x"])


# standard solution of cos(x)
def cos_compute_func(data: dict):
    return np.cos(data["x"])


# set constraint on 1D-geometry([-π, π])
ITERS_PER_EPOCH = 100  # use 100 iterations per training epoch
interior_constraint = ppsci.constraint.InteriorConstraint(
    output_expr={"du_dx": lambda out: jacobian(out["u"], out["x"])},
    label_dict={"du_dx": cos_compute_func},
    geom=x_domain,
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 32,  # use 32 samples(points) per iteration for interior constraint
    },
    loss=ppsci.loss.MSELoss(),
)
bc_constraint = ppsci.constraint.BoundaryConstraint(
    {"u": lambda d: d["u"]},
    {"u": lambda d: sin_compute_func(d) + 2},  # (1)
    x_domain,
    dataloader_cfg={
        "dataset": "NamedArrayDataset",
        "iters_per_epoch": ITERS_PER_EPOCH,
        "sampler": {
            "name": "BatchSampler",
            "shuffle": True,
        },
        "batch_size": 1,  # use 1 sample(point) per iteration for boundary constraint
    },
    loss=ppsci.loss.MSELoss(),
    criteria=lambda x: np.isclose(x, l_limit),
)
# wrap constraint(s) into one dict
constraint = {
    interior_constraint.name: interior_constraint,
    bc_constraint.name: bc_constraint,
}

# set training hyper-parameters
EPOCHS = 10
# set optimizer
optimizer = ppsci.optimizer.Adam(2e-3)(model)

# set visualizer
visual_input_dict = {
    "x": np.linspace(l_limit, r_limit, 1000, dtype="float32").reshape(1000, 1)
}
visual_input_dict["u_ref"] = np.sin(visual_input_dict["x"]) + 2.0
visualizer = {
    "visualize_u": ppsci.visualize.VisualizerScatter1D(
        visual_input_dict,
        ("x",),
        {"u_pred": lambda out: out["u"], "u_ref": lambda out: out["u_ref"]},
        prefix="u=sin(x)",
    ),
}

# initialize solver
solver = ppsci.solver.Solver(
    model,
    constraint,
    OUTPUT_DIR,
    optimizer,
    epochs=EPOCHS,
    iters_per_epoch=ITERS_PER_EPOCH,
    visualizer=visualizer,
)
# train model
solver.train()

# compute l2-relative error of trained model
pred_u = solver.predict(visual_input_dict, return_numpy=True)["u"]
l2_rel = np.linalg.norm(pred_u - visual_input_dict["u_ref"]) / np.linalg.norm(
    visual_input_dict["u_ref"]
)
logger.info(f"l2_rel = {l2_rel:.5f}")

# visualize prediction after finished training
solver.visualize()