跳转至

PhyGeoNet

AI Studio快速体验

# heat_equation
# linux
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation.npz -P ./data/

# windows
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation.npz --create-dirs -o ./data/heat_equation.npz

python heat_equation.py

# heat_equation_bc
# linux
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation_bc.npz -P ./data/
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation_bc_test.npz -P ./data/

# windows
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation_bc.npz --create-dirs -o ./data/heat_equation.npz
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation_bc_test.npz --create-dirs -o ./data/heat_equation.npz

python heat_equation_with_bc.py

# heat_equation
# linux
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation.npz -P ./data/

# windows
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation.npz --create-dirs -o ./data/heat_equation.npz

python heat_equation.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/PhyGeoNet/heat_equation_pretrain.pdparams

# heat_equation_bc
# linux
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation_bc.npz -P ./data/
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation_bc_test.npz -P ./data/

# windows
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation_bc.npz --create-dirs -o ./data/heat_equation.npz
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyGeoNet/heat_equation_bc_test.npz --create-dirs -o ./data/heat_equation.npz

python heat_equation_with_bc.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/PhyGeoNet/heat_equation_bc_pretrain.pdparams
模型 mRes ev
heat_equation_pretrain.pdparams 0.815 0.095
heat_equation_bc_pretrain.pdparams 992 0.31

1. 背景简介

最近几年，深度学习在很多领域取得了非凡的成就，尤其是计算机视觉和自然语言处理方面，受启发于深度学习的快速发展，基于深度学习强大的函数逼近能力，神经网络在科学计算领域也取得了成功，现阶段的研究主要分为两大类，一类是将物理信息以及物理限制加入损失函数来对神经网络进行训练, 其代表有 PINN 以及 Deep Ritz Net，另一类是通过数据驱动的深度神经网络算子，其代表有 FNO 以及 DeepONet。这些方法都在科学实践中获得了广泛应用，比如天气预测，量子化学，生物工程，以及计算流体等领域。由于卷积神经网络具有参数共享的性质，可以学习大尺度的时空域，因此获得了越来越多的关注。

2. 问题定义

而在实际科学计算问题中，很多偏微分方程的求解域是复杂边界且非均匀的。现有神经网络往往针对具有规则边界以及均匀网格的求解域，所以并没有实际应用效果。

本文针对物理信息神经网络在复杂边界非均匀网格求解域上效果较差的问题，提出了通过坐标变化将不规则边界非均匀网格变成规则边界均匀网格的方法，除此之外，本文利用变成均匀网格后，卷积神经网络的上述优势，提出相对应的的物理信息卷积神经网络。

3. 问题求解

为节约篇幅，接下来将以 heat equation 为例讲解如何使用 PaddleScience 进行实现。

3.1 模型构建

本案例使用提出的 USCNN 模型进行训练，该模型的构建入方式如下所示。

23
model = ppsci.arch.USCNN(**cfg.MODEL)

其中，构建模型所需的参数可以从对应的配置文件中获取。

34
35
36
37
38
39
40
41
42
43
MODEL:
  input_keys: [ 'coords' ]
  output_keys: [ 'output_v' ]
  hidden_size: [16, 32, 16]
  h: 0.01
  ny: 19
  nx: 84
  nvar_in: 2
  nvar_out: 1
  pad_singleside: 1

3.2 数据读取

本案例使用的数据集存储在 .npz 文件中，使用如下的代码进行读取。

15
16
17
18
19
20
21
data = np.load(cfg.data_dir)
coords = data["coords"]
jinvs = data["jinvs"]
dxdxis = data["dxdxis"]
dydxis = data["dydxis"]
dxdetas = data["dxdetas"]
dydetas = data["dydetas"]

3.3 输出转化函数构建

本文为强制边界约束，在训练时使用相对应的输出转化函数对模型的输出结果计算微分。

50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
sup_constraint = {sup_constraint_res.name: sup_constraint_res}

def _transform_out(
    _input: Dict[str, paddle.Tensor],
    _output: Dict[str, paddle.Tensor],
    pad_singleside: int = cfg.MODEL.pad_singleside,
):
    """Calculation residual.

    Args:
        _input (Dict[str, paddle.Tensor]): The input of the model.
        _output (Dict[str, paddle.Tensor]): The output of the model.
        pad_singleside (int, optional): Pad size. Defaults to cfg.MODEL.pad_singleside.
    """
    output_v = _output["output_v"]
    jinv = _input["jinvs"]
    dxdxi = _input["dxdxis"]
    dydxi = _input["dydxis"]
    dxdeta = _input["dxdetas"]
    dydeta = _input["dydetas"]
    output_v[:, 0, -pad_singleside:, pad_singleside:-pad_singleside] = 0
    output_v[:, 0, :pad_singleside, pad_singleside:-pad_singleside] = 1
    output_v[:, 0, pad_singleside:-pad_singleside, -pad_singleside:] = 1
    output_v[:, 0, pad_singleside:-pad_singleside, 0:pad_singleside] = 1
    output_v[:, 0, 0, 0] = 0.5 * (output_v[:, 0, 0, 1] + output_v[:, 0, 1, 0])
    output_v[:, 0, 0, -1] = 0.5 * (output_v[:, 0, 0, -2] + output_v[:, 0, 1, -1])
    dvdx = utils.dfdx(output_v, dydeta, dydxi, jinv)
    d2vdx2 = utils.dfdx(dvdx, dydeta, dydxi, jinv)
    dvdy = utils.dfdy(output_v, dxdxi, dxdeta, jinv)
    d2vdy2 = utils.dfdy(dvdy, dxdxi, dxdeta, jinv)

3.4 约束构建

构建相对应约束条件，由于边界约束为强制约束，约束条件主要为残差约束。

28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
sup_constraint_res = ppsci.constraint.SupervisedConstraint(
    {
        "dataset": {
            "name": "NamedArrayDataset",
            "input": {
                "coords": coords,
                "jinvs": jinvs,
                "dxdxis": dxdxis,
                "dydxis": dydxis,
                "dxdetas": dxdetas,
                "dydetas": dydetas,
            },
        },
        "batch_size": cfg.TRAIN.batch_size,
        "iters_per_epoch": iters_per_epoch,
        "num_workers": 0,
    },
    ppsci.loss.FunctionalLoss(
        lambda out, label, weight: {"residual": out["residual"]}
    ),
    name="residual",

3.5 优化器构建

与论文中描述相同，我们使用恒定学习率 0.001 构造 Adam 优化器。

25
optimizer = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model)

3.6 模型训练

完成上述设置之后，只需要将上述实例化的对象按顺序传递给 ppsci.solver.Solver。

82
83
84
85
86
87
88
model.register_output_transform(_transform_out)
solver = ppsci.solver.Solver(
    model,
    sup_constraint,
    cfg.output_dir,
    optimizer,
    epochs=cfg.epochs,

最后启动训练即可：

90
iters_per_epoch=iters_per_epoch,

3.7 模型评估

在模型训练完成之后，可以使用 evaluate() 函数对训练好的模型进行评估，并可视化。

 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
def evaluate(cfg: DictConfig):
    data = np.load(cfg.data_dir)
    coords = data["coords"]

    ofv_sb = paddle.to_tensor(data["OFV_sb"])

    ## create model
    pad_singleside = cfg.MODEL.pad_singleside
    model = ppsci.arch.USCNN(**cfg.MODEL)
    solver = ppsci.solver.Solver(
        model,
        pretrained_model_path=cfg.EVAL.pretrained_model_path,  ### the path of the model
    )
    output_v = solver.predict({"coords": paddle.to_tensor(coords)})
    output_v = output_v["output_v"]

    output_v[0, 0, -pad_singleside:, pad_singleside:-pad_singleside] = 0
    output_v[0, 0, :pad_singleside, pad_singleside:-pad_singleside] = 1
    output_v[0, 0, pad_singleside:-pad_singleside, -pad_singleside:] = 1
    output_v[0, 0, pad_singleside:-pad_singleside, 0:pad_singleside] = 1
    output_v[0, 0, 0, 0] = 0.5 * (output_v[0, 0, 0, 1] + output_v[0, 0, 1, 0])
    output_v[0, 0, 0, -1] = 0.5 * (output_v[0, 0, 0, -2] + output_v[0, 0, 1, -1])

    ev = paddle.sqrt(
        paddle.mean((ofv_sb - output_v[0, 0]) ** 2) / paddle.mean(ofv_sb**2)
    ).item()
    logger.info(f"ev: {ev}")

    output_v = output_v.numpy()
    ofv_sb = ofv_sb.numpy()
    fig = plt.figure()
    ax = plt.subplot(1, 2, 1)
    utils.visualize(
        ax,
        coords[0, 0, 1:-1, 1:-1],
        coords[0, 1, 1:-1, 1:-1],
        output_v[0, 0, 1:-1, 1:-1],
        "horizontal",
        [0, 1],
    )
    utils.set_axis_label(ax, "p")
    ax.set_title("CNN " + r"$T$")
    ax.set_aspect("equal")
    ax = plt.subplot(1, 2, 2)
    utils.visualize(
        ax,
        coords[0, 0, 1:-1, 1:-1],
        coords[0, 1, 1:-1, 1:-1],
        ofv_sb[1:-1, 1:-1],
        "horizontal",
        [0, 1],
    )
    utils.set_axis_label(ax, "p")
    ax.set_aspect("equal")
    ax.set_title("FV " + r"$T$")
    fig.tight_layout(pad=1)

4. 完整代码

heat_equation.py
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
from typing import Dict

import hydra
import matplotlib.pyplot as plt
import numpy as np
import paddle
import utils
from omegaconf import DictConfig

import ppsci
from ppsci.utils import logger


def train(cfg: DictConfig):
    data = np.load(cfg.data_dir)
    coords = data["coords"]
    jinvs = data["jinvs"]
    dxdxis = data["dxdxis"]
    dydxis = data["dydxis"]
    dxdetas = data["dxdetas"]
    dydetas = data["dydetas"]

    model = ppsci.arch.USCNN(**cfg.MODEL)

    optimizer = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model)

    iters_per_epoch = coords.shape[0]
    sup_constraint_res = ppsci.constraint.SupervisedConstraint(
        {
            "dataset": {
                "name": "NamedArrayDataset",
                "input": {
                    "coords": coords,
                    "jinvs": jinvs,
                    "dxdxis": dxdxis,
                    "dydxis": dydxis,
                    "dxdetas": dxdetas,
                    "dydetas": dydetas,
                },
            },
            "batch_size": cfg.TRAIN.batch_size,
            "iters_per_epoch": iters_per_epoch,
            "num_workers": 0,
        },
        ppsci.loss.FunctionalLoss(
            lambda out, label, weight: {"residual": out["residual"]}
        ),
        name="residual",
    )
    sup_constraint = {sup_constraint_res.name: sup_constraint_res}

    def _transform_out(
        _input: Dict[str, paddle.Tensor],
        _output: Dict[str, paddle.Tensor],
        pad_singleside: int = cfg.MODEL.pad_singleside,
    ):
        """Calculation residual.

        Args:
            _input (Dict[str, paddle.Tensor]): The input of the model.
            _output (Dict[str, paddle.Tensor]): The output of the model.
            pad_singleside (int, optional): Pad size. Defaults to cfg.MODEL.pad_singleside.
        """
        output_v = _output["output_v"]
        jinv = _input["jinvs"]
        dxdxi = _input["dxdxis"]
        dydxi = _input["dydxis"]
        dxdeta = _input["dxdetas"]
        dydeta = _input["dydetas"]
        output_v[:, 0, -pad_singleside:, pad_singleside:-pad_singleside] = 0
        output_v[:, 0, :pad_singleside, pad_singleside:-pad_singleside] = 1
        output_v[:, 0, pad_singleside:-pad_singleside, -pad_singleside:] = 1
        output_v[:, 0, pad_singleside:-pad_singleside, 0:pad_singleside] = 1
        output_v[:, 0, 0, 0] = 0.5 * (output_v[:, 0, 0, 1] + output_v[:, 0, 1, 0])
        output_v[:, 0, 0, -1] = 0.5 * (output_v[:, 0, 0, -2] + output_v[:, 0, 1, -1])
        dvdx = utils.dfdx(output_v, dydeta, dydxi, jinv)
        d2vdx2 = utils.dfdx(dvdx, dydeta, dydxi, jinv)
        dvdy = utils.dfdy(output_v, dxdxi, dxdeta, jinv)
        d2vdy2 = utils.dfdy(dvdy, dxdxi, dxdeta, jinv)
        continuity = d2vdy2 + d2vdx2
        return {"residual": paddle.mean(continuity**2)}

    model.register_output_transform(_transform_out)
    solver = ppsci.solver.Solver(
        model,
        sup_constraint,
        cfg.output_dir,
        optimizer,
        epochs=cfg.epochs,
        iters_per_epoch=iters_per_epoch,
    )
    solver.train()
    solver.plot_loss_history()


def evaluate(cfg: DictConfig):
    data = np.load(cfg.data_dir)
    coords = data["coords"]

    ofv_sb = paddle.to_tensor(data["OFV_sb"])

    ## create model
    pad_singleside = cfg.MODEL.pad_singleside
    model = ppsci.arch.USCNN(**cfg.MODEL)
    solver = ppsci.solver.Solver(
        model,
        pretrained_model_path=cfg.EVAL.pretrained_model_path,  ### the path of the model
    )
    output_v = solver.predict({"coords": paddle.to_tensor(coords)})
    output_v = output_v["output_v"]

    output_v[0, 0, -pad_singleside:, pad_singleside:-pad_singleside] = 0
    output_v[0, 0, :pad_singleside, pad_singleside:-pad_singleside] = 1
    output_v[0, 0, pad_singleside:-pad_singleside, -pad_singleside:] = 1
    output_v[0, 0, pad_singleside:-pad_singleside, 0:pad_singleside] = 1
    output_v[0, 0, 0, 0] = 0.5 * (output_v[0, 0, 0, 1] + output_v[0, 0, 1, 0])
    output_v[0, 0, 0, -1] = 0.5 * (output_v[0, 0, 0, -2] + output_v[0, 0, 1, -1])

    ev = paddle.sqrt(
        paddle.mean((ofv_sb - output_v[0, 0]) ** 2) / paddle.mean(ofv_sb**2)
    ).item()
    logger.info(f"ev: {ev}")

    output_v = output_v.numpy()
    ofv_sb = ofv_sb.numpy()
    fig = plt.figure()
    ax = plt.subplot(1, 2, 1)
    utils.visualize(
        ax,
        coords[0, 0, 1:-1, 1:-1],
        coords[0, 1, 1:-1, 1:-1],
        output_v[0, 0, 1:-1, 1:-1],
        "horizontal",
        [0, 1],
    )
    utils.set_axis_label(ax, "p")
    ax.set_title("CNN " + r"$T$")
    ax.set_aspect("equal")
    ax = plt.subplot(1, 2, 2)
    utils.visualize(
        ax,
        coords[0, 0, 1:-1, 1:-1],
        coords[0, 1, 1:-1, 1:-1],
        ofv_sb[1:-1, 1:-1],
        "horizontal",
        [0, 1],
    )
    utils.set_axis_label(ax, "p")
    ax.set_aspect("equal")
    ax.set_title("FV " + r"$T$")
    fig.tight_layout(pad=1)
    fig.savefig(f"{cfg.output_dir}/result.png", bbox_inches="tight")
    plt.close(fig)


@hydra.main(version_base=None, config_path="./conf", config_name="heat_equation.yaml")
def main(cfg: DictConfig):
    if cfg.mode == "train":
        train(cfg)
    elif cfg.mode == "eval":
        evaluate(cfg)
    else:
        raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'")


if __name__ == "__main__":
    main()

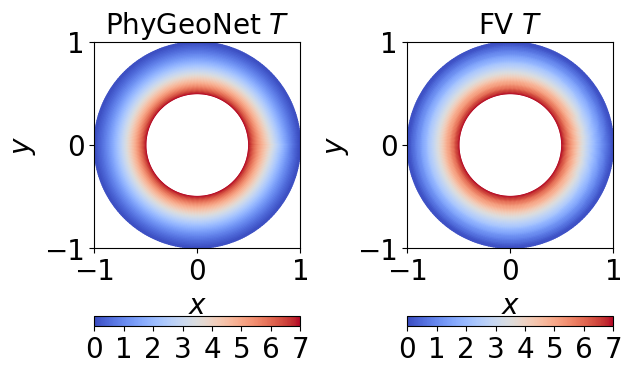
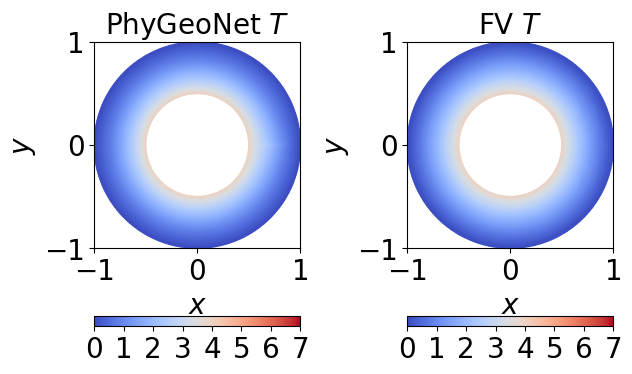
5. 结果展示

Heat equation结果展示: image

Heat equation with boundary 结果展示：

T=0 image

T=3 image

T=6 iamge

6. 总结

本文通过使用调和映射构造坐标变换函数，使得物理信息网络可以在不规则非均匀网格上面进行训练，同时，因为该映射为使用传统方法进行，所以无需训练即可在网络前后嵌入。通过大量实验表明，该网络可以在各种不规则网格问题上表现比SOAT网络突出。

7. 参考资料

PhyGeoNet: Physics-informed geometry-adaptive convolutional neural networks for solving parameterized steady-state PDEs on irregular domain

Github PhyGeoNet