跳转至

Allen-Cahn

AI Studio快速体验

# linux
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/AllenCahn/allen_cahn.mat -P ./dataset/
# windows
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/AllenCahn/allen_cahn.mat --create-dirs -o ./dataset/allen_cahn.mat
python allen_cahn_piratenet.py

# linux
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/AllenCahn/allen_cahn.mat -P ./dataset/
# windows
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/AllenCahn/allen_cahn.mat --create-dirs -o ./dataset/allen_cahn.mat
python allen_cahn_piratenet.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/AllenCahn/allen_cahn_piratenet_pretrained.pdparams

python allen_cahn_piratenet.py mode=export

# linux
wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/AllenCahn/allen_cahn.mat -P ./dataset/
# windows
# curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/AllenCahn/allen_cahn.mat --create-dirs -o ./dataset/allen_cahn.mat
python allen_cahn_piratenet.py mode=infer
预训练模型 指标
allen_cahn_piratenet_pretrained.pdparams L2Rel.u: 1.2e-05

1. 背景简介

Allen-Cahn 方程（有时也叫作模型方程或相场方程）是一种数学模型，通常用于描述两种不同相之间的界面演化。这个方程最早由Samuel Allen和John Cahn在1970年代提出，用以描述合金中相分离的过程。Allen-Cahn 方程是一种非线性偏微分方程，其一般形式可以写为：

\[ \frac{\partial u}{\partial t} = \varepsilon^2 \Delta u - F'(u) \]

这里：

  • \(u(\mathbf{x},t)\) 是一个场变量，代表某个物理量，例如合金的组分浓度或者晶体中的有序参数。
  • \(t\) 表示时间。
  • \(\mathbf{x}\) 表示空间位置。
  • \(\Delta\) 是Laplace算子，对应于空间变量的二阶偏导数（即 \(\Delta u = \nabla^2 u\) ），用来描述空间扩散过程。
  • \(\varepsilon\) 是一个正的小参数，它与相界面的宽度相关。
  • \(F(u)\) 是一个双稳态势能函数，通常取为\(F(u) = \frac{1}{4}(u^2-1)^2\)，这使得 \(F'(u) = u^3 - u\) 是其导数，这代表了非线性的反应项，负责驱动系统向稳定状态演化。

这个方程中的 \(F'(u)\) 项使得在 \(u=1\) 和 \(u=-1\) 附近有两个稳定的平衡态，这对应于不同的物理相。而 \(\varepsilon^2 \Delta u\) 项则描述了相界面的曲率引起的扩散效应，这导致界面趋向于减小曲率。因此，Allen-Cahn 方程描述了由于相界面曲率和势能影响而发生的相变。

在实际应用中，该方程还可能包含边界条件和初始条件，以便对特定问题进行数值模拟和分析。例如，在特定的物理问题中，可能会有 Neumann 边界条件（导数为零，表示无通量穿过边界）或 Dirichlet 边界条件（固定的边界值）。

本案例解决以下 Allen-Cahn 方程：

\[ \begin{aligned} & u_t - 0.0001 u_{xx} + 5 u^3 - 5 u = 0,\quad t \in [0, 1],\ x\in[-1, 1],\\ &u(x,0) = x^2 \cos(\pi x),\\ &u(t, -1) = u(t, 1),\\ &u_x(t, -1) = u_x(t, 1). \end{aligned} \]

2. 问题定义

根据上述方程，可知计算域为\([0, 1]\times [-1, 1]\)，含有一个初始条件： \(u(x,0) = x^2 \cos(\pi x)\)，两个周期边界条件：\(u(t, -1) = u(t, 1)\)、\(u_x(t, -1) = u_x(t, 1)\)。

3. 问题求解

接下来开始讲解如何将问题一步一步地转化为 PaddleScience 代码，用深度学习的方法求解该问题。 为了快速理解 PaddleScience，接下来仅对模型构建、方程构建、计算域构建等关键步骤进行阐述，而其余细节请参考 API文档。

3.1 模型构建

在 Allen-Cahn 问题中，每一个已知的坐标点 \((t, x)\) 都有对应的待求解的未知量 \((u)\)， ，在这里使用 PirateNet 来表示 \((t, x)\) 到 \((u)\) 的映射函数 \(f: \mathbb{R}^2 \to \mathbb{R}^1\) ，即：

\[ u = f(t, x) \]

上式中 \(f\) 即为 PirateNet 模型本身，用 PaddleScience 代码表示如下

63
64
# set model
model = ppsci.arch.PirateNet(**cfg.MODEL)

为了在计算时，准确快速地访问具体变量的值，在这里指定网络模型的输入变量名是 ("t", "x")，输出变量名是 ("u")，这些命名与后续代码保持一致。

接着通过指定 PirateNet 的层数、神经元个数，就实例化出了一个拥有 3 个 PiraBlock，每个 PiraBlock 的隐层神经元个数为 256 的神经网络模型 model， 并且使用 tanh 作为激活函数。

34
35
36
37
38
39
40
# model settings
MODEL:
  input_keys: [t, x]
  output_keys: [u]
  num_blocks: 3
  hidden_size: 256
  activation: tanh

3.2 方程构建

Allen-Cahn 微分方程可以用如下代码表示：

66
67
# set equation
equation = {"AllenCahn": ppsci.equation.AllenCahn(eps=0.01)}

3.3 计算域构建

本问题的计算域为 \([0, 1]\times [-1, 1]\)，其中用于训练的数据已提前生成，保存在 ./dataset/allen_cahn.mat 中，读取并生成计算域内的离散点。

69
70
71
72
73
74
75
76
77
78
79
80
81
# set constraint
data = sio.loadmat(cfg.DATA_PATH)
u_ref = data["usol"].astype(dtype)  # (nt, nx)
t_star = data["t"].flatten().astype(dtype)  # [nt, ]
x_star = data["x"].flatten().astype(dtype)  # [nx, ]

u0 = u_ref[0, :]  # [nx, ]

t0 = t_star[0]  # float
t1 = t_star[-1]  # float

x0 = x_star[0]  # float
x1 = x_star[-1]  # float

3.4 约束构建

3.4.1 内部点约束

以作用在内部点上的 SupervisedConstraint 为例，代码如下：

 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
def gen_label_batch(input_batch):
    return {"allen_cahn": np.zeros([cfg.TRAIN.batch_size, 1], dtype)}

pde_constraint = ppsci.constraint.SupervisedConstraint(
    {
        "dataset": {
            "name": "ContinuousNamedArrayDataset",
            "input": gen_input_batch,
            "label": gen_label_batch,
        },
    },
    output_expr=equation["AllenCahn"].equations,
    loss=ppsci.loss.CausalMSELoss(
        cfg.TRAIN.causal.n_chunks, "mean", tol=cfg.TRAIN.causal.tol
    ),
    name="PDE",
)

SupervisedConstraint 的第一个参数是用于训练的数据配置，由于我们使用实时随机生成的数据，而不是固定数据点，因此填入自定义的输入数据/标签生成函数；

第二个参数是方程表达式，因此传入 Allen-Cahn 的方程对象；

第三个参数是损失函数，此处选用 CausalMSELoss 函数，其会根据 causal 和 tol 参数，对不同的时间窗口进行重新加权， 能更好地优化瞬态问题；

第四个参数是约束条件的名字，需要给每一个约束条件命名，方便后续对其索引。此处命名为 "PDE" 即可。

3.4.2 周期边界约束

此处我们采用 hard-constraint 的方式，在神经网络模型中，对输入数据使用cos、sin等周期函数进行周期化，从而让\(u_{\theta}\)在数学上直接满足方程的周期性质。 根据方程可得函数\(u(t, x)\)在\(x\)轴上的周期为 2，因此将该周期设置到模型配置里即可。

41
42
periods:
  x: [2.0, false]

3.4.3 初值约束

第三个约束条件是初值约束，代码如下：

112
113
114
115
116
117
118
119
120
121
122
123
124
125
ic_input = {"t": np.full([len(x_star), 1], t0), "x": x_star.reshape([-1, 1])}
ic_label = {"u": u0.reshape([-1, 1])}
ic = ppsci.constraint.SupervisedConstraint(
    {
        "dataset": {
            "name": "IterableNamedArrayDataset",
            "input": ic_input,
            "label": ic_label,
        },
    },
    output_expr={"u": lambda out: out["u"]},
    loss=ppsci.loss.MSELoss("mean"),
    name="IC",
)

在微分方程约束、初值约束构建完毕之后，以刚才的命名为关键字，封装到一个字典中，方便后续访问。

126
127
128
129
130
# wrap constraints together
constraint = {
    pde_constraint.name: pde_constraint,
    ic.name: ic,
}

3.5 超参数设定

接下来需要指定训练轮数和学习率，此处按实验经验，使用 300 轮训练轮数，0.001 的初始学习率。

50
51
52
53
54
55
56
57
58
59
60
61
62
63
# training settings
TRAIN:
  epochs: 300
  iters_per_epoch: 1000
  save_freq: 10
  eval_during_train: true
  eval_freq: 10
  lr_scheduler:
    epochs: ${TRAIN.epochs}
    iters_per_epoch: ${TRAIN.iters_per_epoch}
    learning_rate: 1.0e-3
    gamma: 0.9
    decay_steps: 5000
    by_epoch: false

3.6 优化器构建

训练过程会调用优化器来更新模型参数，此处选择较为常用的 Adam 优化器，并配合使用机器学习中常用的 ExponentialDecay 学习率调整策略。

132
133
134
135
136
# set optimizer
lr_scheduler = ppsci.optimizer.lr_scheduler.ExponentialDecay(
    **cfg.TRAIN.lr_scheduler
)()
optimizer = ppsci.optimizer.Adam(lr_scheduler)(model)

3.7 评估器构建

在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，因此使用 ppsci.validate.SupervisedValidator 构建评估器。

138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
# set validator
tx_star = misc.cartesian_product(t_star, x_star).astype(dtype)
eval_data = {"t": tx_star[:, 0:1], "x": tx_star[:, 1:2]}
eval_label = {"u": u_ref.reshape([-1, 1])}
u_validator = ppsci.validate.SupervisedValidator(
    {
        "dataset": {
            "name": "NamedArrayDataset",
            "input": eval_data,
            "label": eval_label,
        },
        "batch_size": cfg.EVAL.batch_size,
    },
    ppsci.loss.MSELoss("mean"),
    {"u": lambda out: out["u"]},
    metric={"L2Rel": ppsci.metric.L2Rel()},
    name="u_validator",
)
validator = {u_validator.name: u_validator}

3.9 模型训练、评估与可视化

完成上述设置之后，只需要将上述实例化的对象按顺序传递给 ppsci.solver.Solver，然后启动训练、评估、可视化。

158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
# initialize solver
solver = ppsci.solver.Solver(
    model,
    constraint,
    optimizer=optimizer,
    equation=equation,
    validator=validator,
    loss_aggregator=mtl.GradNorm(
        model,
        len(constraint),
        cfg.TRAIN.grad_norm.update_freq,
        cfg.TRAIN.grad_norm.momentum,
    ),
    cfg=cfg,
)
# train model
solver.train()
# evaluate after finished training
solver.eval()
# visualize prediction after finished training
u_pred = solver.predict(
    eval_data, batch_size=cfg.EVAL.batch_size, return_numpy=True
)["u"]
u_pred = u_pred.reshape([len(t_star), len(x_star)])

# plot
plot(t_star, x_star, u_ref, u_pred, cfg.output_dir)

4. 完整代码

allen_cahn_piratenet.py
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
"""
Reference: https://github.com/PredictiveIntelligenceLab/jaxpi/tree/main/examples/allen_cahn
"""

from os import path as osp

import hydra
import numpy as np
import paddle
import scipy.io as sio
from matplotlib import pyplot as plt
from omegaconf import DictConfig

import ppsci
from ppsci.loss import mtl
from ppsci.utils import misc

dtype = paddle.get_default_dtype()


def plot(
    t_star: np.ndarray,
    x_star: np.ndarray,
    u_ref: np.ndarray,
    u_pred: np.ndarray,
    output_dir: str,
):
    fig = plt.figure(figsize=(18, 5))
    TT, XX = np.meshgrid(t_star, x_star, indexing="ij")
    u_ref = u_ref.reshape([len(t_star), len(x_star)])

    plt.subplot(1, 3, 1)
    plt.pcolor(TT, XX, u_ref, cmap="jet")
    plt.colorbar()
    plt.xlabel("t")
    plt.ylabel("x")
    plt.title("Exact")
    plt.tight_layout()

    plt.subplot(1, 3, 2)
    plt.pcolor(TT, XX, u_pred, cmap="jet")
    plt.colorbar()
    plt.xlabel("t")
    plt.ylabel("x")
    plt.title("Predicted")
    plt.tight_layout()

    plt.subplot(1, 3, 3)
    plt.pcolor(TT, XX, np.abs(u_ref - u_pred), cmap="jet")
    plt.colorbar()
    plt.xlabel("t")
    plt.ylabel("x")
    plt.title("Absolute error")
    plt.tight_layout()

    fig_path = osp.join(output_dir, "ac.png")
    print(f"Saving figure to {fig_path}")
    fig.savefig(fig_path, bbox_inches="tight", dpi=400)
    plt.close()


def train(cfg: DictConfig):
    # set model
    model = ppsci.arch.PirateNet(**cfg.MODEL)

    # set equation
    equation = {"AllenCahn": ppsci.equation.AllenCahn(eps=0.01)}

    # set constraint
    data = sio.loadmat(cfg.DATA_PATH)
    u_ref = data["usol"].astype(dtype)  # (nt, nx)
    t_star = data["t"].flatten().astype(dtype)  # [nt, ]
    x_star = data["x"].flatten().astype(dtype)  # [nx, ]

    u0 = u_ref[0, :]  # [nx, ]

    t0 = t_star[0]  # float
    t1 = t_star[-1]  # float

    x0 = x_star[0]  # float
    x1 = x_star[-1]  # float

    def gen_input_batch():
        tx = np.random.uniform(
            [t0, x0],
            [t1, x1],
            (cfg.TRAIN.batch_size, 2),
        ).astype(dtype)
        return {
            "t": np.sort(tx[:, 0:1], axis=0),
            "x": tx[:, 1:2],
        }

    def gen_label_batch(input_batch):
        return {"allen_cahn": np.zeros([cfg.TRAIN.batch_size, 1], dtype)}

    pde_constraint = ppsci.constraint.SupervisedConstraint(
        {
            "dataset": {
                "name": "ContinuousNamedArrayDataset",
                "input": gen_input_batch,
                "label": gen_label_batch,
            },
        },
        output_expr=equation["AllenCahn"].equations,
        loss=ppsci.loss.CausalMSELoss(
            cfg.TRAIN.causal.n_chunks, "mean", tol=cfg.TRAIN.causal.tol
        ),
        name="PDE",
    )

    ic_input = {"t": np.full([len(x_star), 1], t0), "x": x_star.reshape([-1, 1])}
    ic_label = {"u": u0.reshape([-1, 1])}
    ic = ppsci.constraint.SupervisedConstraint(
        {
            "dataset": {
                "name": "IterableNamedArrayDataset",
                "input": ic_input,
                "label": ic_label,
            },
        },
        output_expr={"u": lambda out: out["u"]},
        loss=ppsci.loss.MSELoss("mean"),
        name="IC",
    )
    # wrap constraints together
    constraint = {
        pde_constraint.name: pde_constraint,
        ic.name: ic,
    }

    # set optimizer
    lr_scheduler = ppsci.optimizer.lr_scheduler.ExponentialDecay(
        **cfg.TRAIN.lr_scheduler
    )()
    optimizer = ppsci.optimizer.Adam(lr_scheduler)(model)

    # set validator
    tx_star = misc.cartesian_product(t_star, x_star).astype(dtype)
    eval_data = {"t": tx_star[:, 0:1], "x": tx_star[:, 1:2]}
    eval_label = {"u": u_ref.reshape([-1, 1])}
    u_validator = ppsci.validate.SupervisedValidator(
        {
            "dataset": {
                "name": "NamedArrayDataset",
                "input": eval_data,
                "label": eval_label,
            },
            "batch_size": cfg.EVAL.batch_size,
        },
        ppsci.loss.MSELoss("mean"),
        {"u": lambda out: out["u"]},
        metric={"L2Rel": ppsci.metric.L2Rel()},
        name="u_validator",
    )
    validator = {u_validator.name: u_validator}

    # initialize solver
    solver = ppsci.solver.Solver(
        model,
        constraint,
        optimizer=optimizer,
        equation=equation,
        validator=validator,
        loss_aggregator=mtl.GradNorm(
            model,
            len(constraint),
            cfg.TRAIN.grad_norm.update_freq,
            cfg.TRAIN.grad_norm.momentum,
        ),
        cfg=cfg,
    )
    # train model
    solver.train()
    # evaluate after finished training
    solver.eval()
    # visualize prediction after finished training
    u_pred = solver.predict(
        eval_data, batch_size=cfg.EVAL.batch_size, return_numpy=True
    )["u"]
    u_pred = u_pred.reshape([len(t_star), len(x_star)])

    # plot
    plot(t_star, x_star, u_ref, u_pred, cfg.output_dir)


def evaluate(cfg: DictConfig):
    # set model
    model = ppsci.arch.PirateNet(**cfg.MODEL)

    data = sio.loadmat(cfg.DATA_PATH)
    u_ref = data["usol"].astype(dtype)  # (nt, nx)
    t_star = data["t"].flatten().astype(dtype)  # [nt, ]
    x_star = data["x"].flatten().astype(dtype)  # [nx, ]

    # set validator
    tx_star = misc.cartesian_product(t_star, x_star).astype(dtype)
    eval_data = {"t": tx_star[:, 0:1], "x": tx_star[:, 1:2]}
    eval_label = {"u": u_ref.reshape([-1, 1])}
    u_validator = ppsci.validate.SupervisedValidator(
        {
            "dataset": {
                "name": "NamedArrayDataset",
                "input": eval_data,
                "label": eval_label,
            },
            "batch_size": cfg.EVAL.batch_size,
        },
        ppsci.loss.MSELoss("mean"),
        {"u": lambda out: out["u"]},
        metric={"L2Rel": ppsci.metric.L2Rel()},
        name="u_validator",
    )
    validator = {u_validator.name: u_validator}

    # initialize solver
    solver = ppsci.solver.Solver(
        model,
        validator=validator,
        cfg=cfg,
    )

    # evaluate after finished training
    solver.eval()
    # visualize prediction after finished training
    u_pred = solver.predict(
        eval_data, batch_size=cfg.EVAL.batch_size, return_numpy=True
    )["u"]
    u_pred = u_pred.reshape([len(t_star), len(x_star)])

    # plot
    plot(t_star, x_star, u_ref, u_pred, cfg.output_dir)


def export(cfg: DictConfig):
    # set model
    model = ppsci.arch.PirateNet(**cfg.MODEL)

    # initialize solver
    solver = ppsci.solver.Solver(model, cfg=cfg)
    # export model
    from paddle.static import InputSpec

    input_spec = [
        {key: InputSpec([None, 1], "float32", name=key) for key in model.input_keys},
    ]
    solver.export(input_spec, cfg.INFER.export_path, with_onnx=False)


def inference(cfg: DictConfig):
    from deploy.python_infer import pinn_predictor

    predictor = pinn_predictor.PINNPredictor(cfg)
    data = sio.loadmat(cfg.DATA_PATH)
    u_ref = data["usol"].astype(dtype)  # (nt, nx)
    t_star = data["t"].flatten().astype(dtype)  # [nt, ]
    x_star = data["x"].flatten().astype(dtype)  # [nx, ]
    tx_star = misc.cartesian_product(t_star, x_star).astype(dtype)

    input_dict = {"t": tx_star[:, 0:1], "x": tx_star[:, 1:2]}
    output_dict = predictor.predict(input_dict, cfg.INFER.batch_size)
    # mapping data to cfg.INFER.output_keys
    output_dict = {
        store_key: output_dict[infer_key]
        for store_key, infer_key in zip(cfg.MODEL.output_keys, output_dict.keys())
    }
    u_pred = output_dict["u"].reshape([len(t_star), len(x_star)])

    plot(t_star, x_star, u_ref, u_pred, cfg.output_dir)


@hydra.main(
    version_base=None, config_path="./conf", config_name="allen_cahn_piratenet.yaml"
)
def main(cfg: DictConfig):
    if cfg.mode == "train":
        train(cfg)
    elif cfg.mode == "eval":
        evaluate(cfg)
    elif cfg.mode == "export":
        export(cfg)
    elif cfg.mode == "infer":
        inference(cfg)
    else:
        raise ValueError(
            f"cfg.mode should in ['train', 'eval', 'export', 'infer'], but got '{cfg.mode}'"
        )


if __name__ == "__main__":
    main()

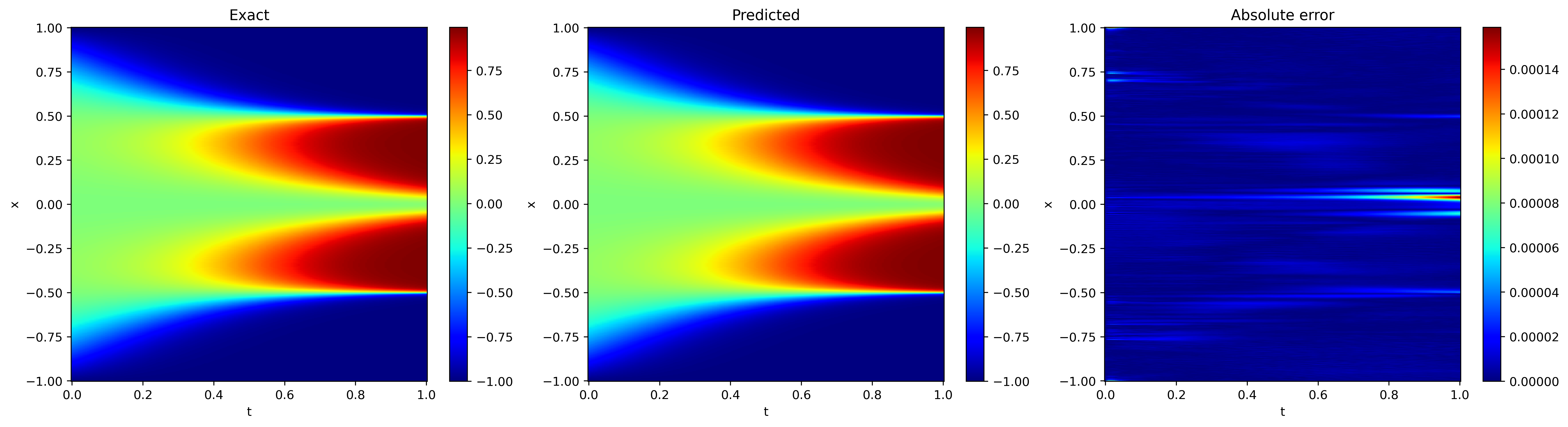
5. 结果展示

在计算域上均匀采样出 \(201\times501\) 个点，其预测结果和解析解如下图所示。

allen_cahn_piratenet.jpg

左侧为 PaddleScience 预测结果，中间为解析解结果，右侧为两者的差值

可以看到对于函数\(u(t, x)\)，模型的预测结果和解析解的结果基本一致。

6. 参考资料